Verification Case 01: Elliptical fire shape

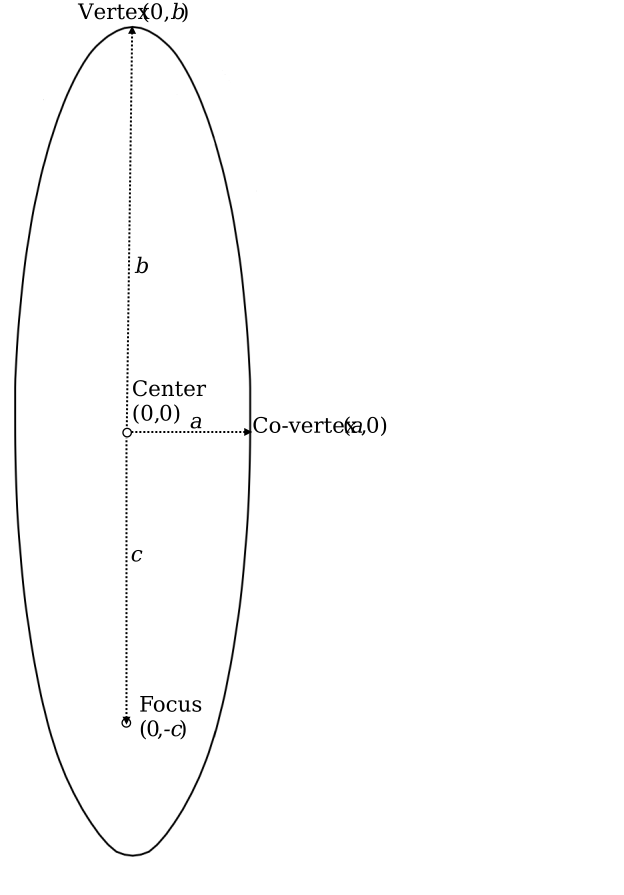
Consider an ellipse centered at (0,0) with its minor axis oriented in the x direction and its major axis oriented in the y direction. Some relevant geometrical nomenclature and coordinates include:

• Center: (0,0)

• Vertices: (0,b) and (0,-b)

• Co-vertices: (a,0) and (-a,0)

• Foci: (0,c) and (0,-c)

With these definitions, the area of the ellipse is:

\[A = \pi ab\]

For a point source ignition and the simplified case of fire spreading in the +y direction at constant rate \(V_{head}\), the ellipse focus located at (0,-c) corresponds to the ignition point. Defining \(V_{head}\) as spread rate in the +y direction at (0,b), \(V_{flank}\) becomes spread rate in the +x direction at (a, 0), and \(V_{back}\) is the spread rate in the -y direction at (0, -b). Assuming a constant rate of spread, the relationship between these spread rates, time t, and the elliptical dimensions a, b, and c are:

\[ \begin{align}\begin{aligned}V_{head} × t = b + c\\V_{flank} × t = a\\V_{back} × t = b – c\end{aligned}\end{align} \]

From the above equation, the ratio of \(V_{head}\) to \(V_{back}\) is (b + c) / (b – c) which, from the geometrical properties of an ellipse, is related to its length-to-width ratio (L/W) as:

\[\frac{V_{\text{head}}}{V_{\text{back}}} = \frac{b + c}{b - c} = \frac{\frac{L}{W} + \sqrt{\left( \frac{L}{W} \right)^{2} - 1}}{\frac{L}{W} - \sqrt{\left( \frac{L}{W} \right)^{2} - 1}}\]

With \(V_{head}\) and L/W known (more on this later), \(V_{back}\) can be calculated from the equation above. \(V_{flank}\) is then calculated as:

\[V_{\text{flank}} = \frac{1}{2}\frac{V_{\text{head}} + V_{\text{back}}}{L/W\ }\]

The ellipse length to width ratio (L/W) is usually estimated from empirical observations. Following Anderson (1983), ensuring that L/W = 1 at zero wind speed, and limiting the length to width ratio to 8, L/W can be estimated from mid-flame wind speed (\(U_{mf}\)) in mph as:

\[\frac{L}{W} = \min\left\lbrack 0.936 \times \exp\left( 0.2566U_{\text{mf}} \right) + 0.461 \times \exp\left( - 0.1548U_{\text{mf}} \right) - 0.397,\ 8\ \right\rbrack\]

The equations above can be used to generate an exact solution for the position of the ellipses surface as a function of time. Assuming that the ignition location has coordinates (0, \(y_{ign}\)) the procedure is as follows:

1. Given \(V_{head}\) and L/W, calculate \(V_{back}\) and \(V_{flank}\) using the equations above.

2. For a given time t: Calculate a = \(V_{flank}\) × t, b = a × L/W, and c = \(V_{head}\) × t - b.

3. The center of the ellipse at time t has coordinates (0, \(y_{cen}\)) where \(y_{cen}\) = \(y_{ign}\) + c.

4. Given a value of y (such that \(y_{cen}\) - b <= y <= \(y_{cen}\) + b): Values of x corresponding to the ellipse surface are \(x = a × \sqrt{1 - ((y-y_{cen})/b)^2}\).

To generate exact solutions for ellipse surfaces that can be compared with ELMFIRE’s modeled fire perimeters, we first need to establish values of \(V_{head}\) and L/W. In ELMFIRE, \(V_{head}\) is calculated from the Rothermel model and L/W is calculated from mid-flame wind speed using the above equation. Therefore, we use BehavePlus 6.0.0 Beta 3 to determine Vhead. Inputs to Behave’s surface module are as follows:

• Fuel Model: GR2 (102)

• 1-h fuel moisture: 3%

• Live herbaceous fuel moisture: 30%

• 20-ft wind speed: 10 mph

• Slope steepness: 0%

Corresponding outputs are:

• Surface fire rate of spread: 46.15 ft/min

• Midflame wind speed: 3.62 mph

Plugging \(U_{mf}\) = 3.62 mph into Equation 4 gives L/W = 2.236.

To generate the exact solution perimeters corresponding to the preceding inputs and run the corresponding ELMFIRE validation case do the following:

cd $ELMFIRE_BASE_DIR/verification/01-elliptical-shape
./01-build-ellipse.sh

This will first generate GIS data for the exact solution ellipses using the above procedures. In the ./exact_ellipses directory you will find six shapefiles, each corresponding to the ellipse position from 1 hour to 6 hours at an hourly interval. This script next runs the analogous ELMFIRE simulation by executing the ./03-run-elmfire.sh script which takes approximately 60 seconds.

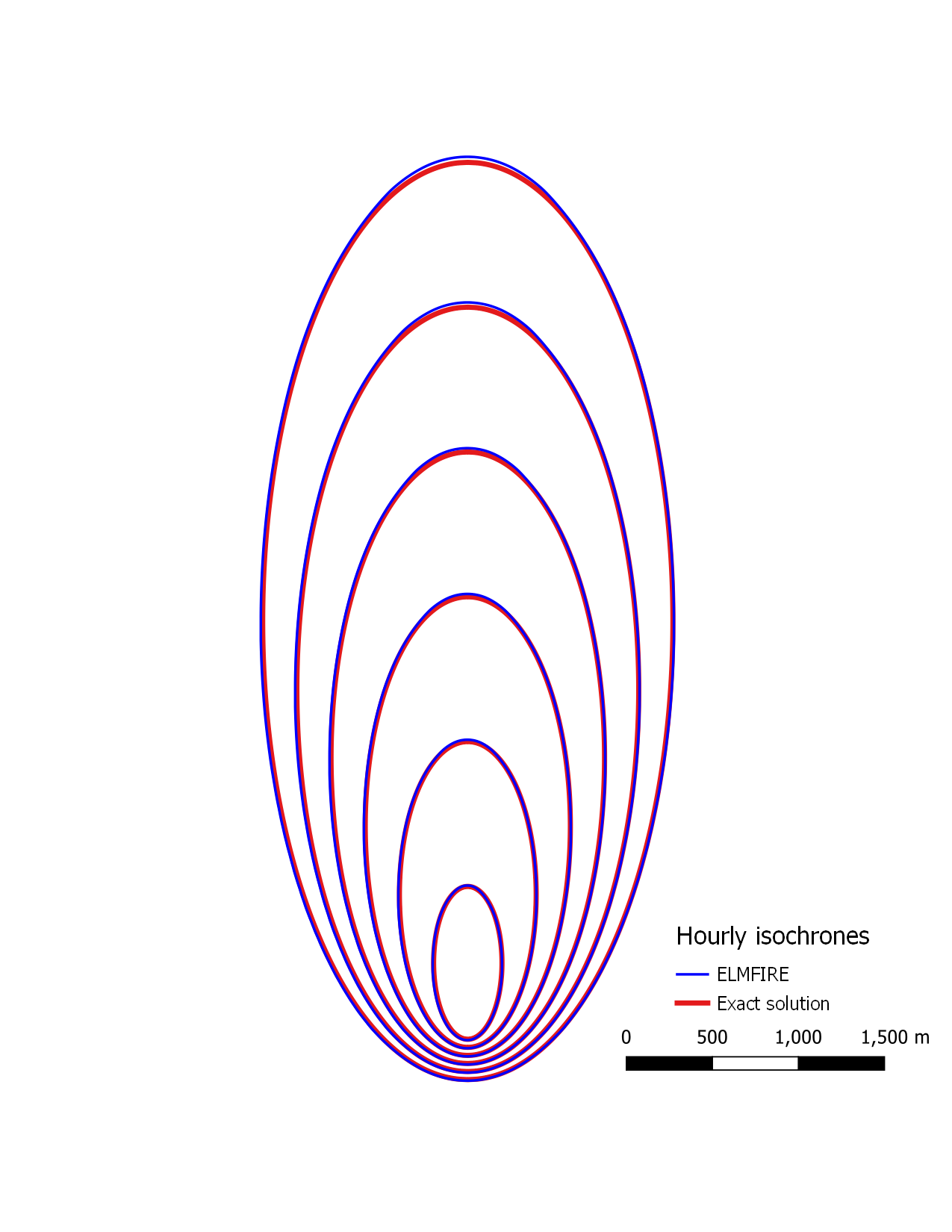
Plotting exact solution ellipses from the exact_ellipses folder against ELMFIRE’s ./outputs/hourly_isochrones.shp file (see Figure below) shows that the numerical (ELMFIRE) and exact solution match to a precision better than 0.5%. This is typical in wildfire modeling - error and uncertainty introduced by underlying numerical methods, providing they are robust and correctly implemented, are small in comparison to other sources of error and uncertainty such as fuel and weather inputs.

Although the main purpose of this verification case is to assess how well the underlying Eulerian Level Set Method as implemented in ELMFIRE is capable of generating idealized elliptical fire shapes, it also preliminarily demonstrates two additional aspects of model verification:

1. The Rothermel model, which provides the head fire spread rate as a function of fuel model, fuel moisture, wind speed, and slope is correctly implemented in ELMFIRE.

2. Since ELMFIRE was provided with only a 20-ft wind speed but the Rothermel model operates on midflame wind speed, the wind adjustment factor that converts 20-ft wind speed to mid-flame wind speed is correctly implemented in ELMFIRE.

Since the above statements are limited to the combinations of inputs used in this verification exercise, these important aspects of model verification are explored in greater detail later.