Suppression

ELMFIRE includes experimental initial attack and extended attack suppression models. These models, both disabled by default, can be configured from the &SUPPRESSION namelist group.

Initial Attack

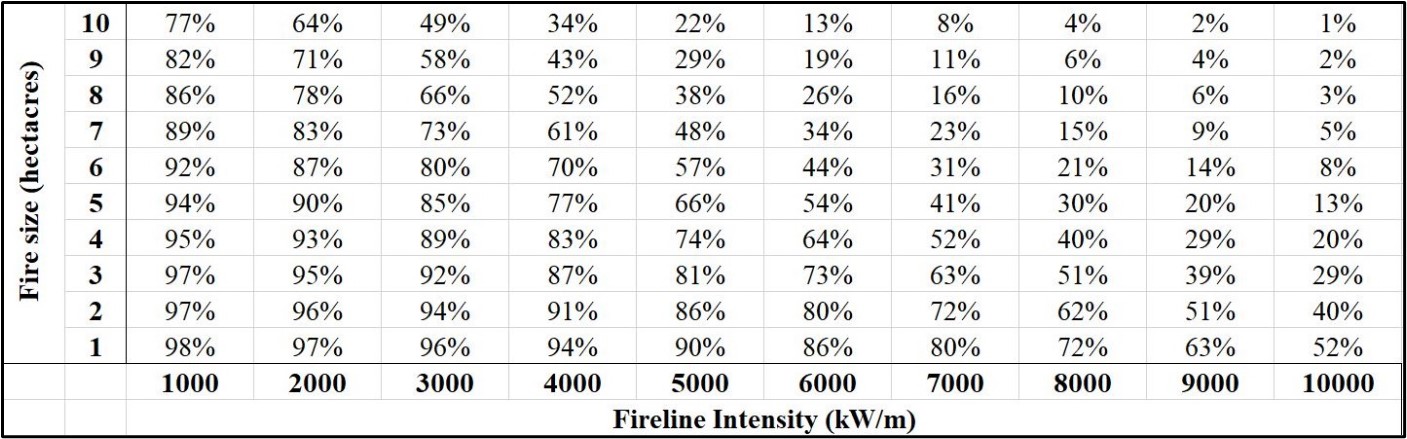
The approach used here to quantify initial attack probability of containment is based on the analysis of `Hirsch et al. <https://academic.oup.com/forestscience/article/44/4/539/4627517`_ who leveraged expert judgment to quantify initial attack effectiveness as a function of fire size and head fire fireline intensity, i.e. intensity at the main advancing fire front, at the time of initial attack commencement. The authors developed an expression for probability of containment (POC) as a function of fire size (A) and fireline intensity (I) which is given in the equation below:

\[POC = \frac{E}{1+E} ln E = 4.6835 - 0.7043A - 0.00041I - 0.000052AI\]

In the equation above, \({A}\) is in hectares and \({I}\) is in kW/m. Since trends in probability of containment are not immediately apparent upon inspection of the equation, probability of containment calculated from the equation is tabulated in the following table as a function of fire size and head fire fireline intensity at the time of initial attack. Although the qualitative trends in the table are logical, i.e. containment probability increases with smaller fires, lower intensity, or both, the `Hirsch et al. <https://academic.oup.com/forestscience/article/44/4/539/4627517`_ study was based on expert opinion from Canadian firefighters so differences in suppression tactics between Canadian and U.S. agencies are not reflected in the table.

In order to use the equation, the time of initial attack commencement relative to the time of fire ignition (\({t_{ign}}\)) must be established for each ignition location. This can be viewed as the sum of fire detection time (\({t_d}\)), report time (\({t_r}\)), and travel time (\({t_t}\)):

\[t_{initial attack} - t_{ign} = t_d + t_r + t_t\]

Initial attack suppression modeling, disabled by default, can be enabled by setting ENABLE_INITIAL_ATTACK=.TRUE.. The time of initial attack commencement, in seconds, must also be specified using the INITIAL_ATTACK_TIME keyword.

Extended Attack

Change in containment (\({\Delta C}\)) during time interval \({\Delta t}\) (in days) is:

\[\frac{\Delta C}{\Delta t} \approx \chi (1 - \frac{logA_d}{logA_{d0}})f(SDI_{\Delta t})\]

where \({Chi}\) is suppression effectiveness coefficient (-), \({A_d}\) is areal growth on a daily basis (acres/day), and \({A_{d0}}\) is areal growth on a daily basis at which containment change becomes negative (acres/day).

The function \({f(SDI_{\Delta t})}\) is calculated from the mean suppression difficulty index during interval \({\Delta t (\bar{SDI_{\Delta t}})}\) as:

\[\begin{equation} f(SDI_{\Delta t}) = \begin{cases} \exp(-B \bar{SDI_{\Delta t}}), & \text{for}\ \frac{\Delta C}{\Delta t}\geq0 0 \exp(B \bar{SDI_{\Delta t}}), & \text{for}\ \frac{\Delta C}{\Delta t} < 0 \end{cases} \end{equation}\]

where \({B}\) is the calibration constant, \({i}\) is the pixel index, \({n}\) is the number of pixels during time interval \({\Delta t}\), and \({SDI_i}\) is the Suppression Difficulty Index of pixel i.

The extended attack model can ben enabled by setting ENABLE_EXTENDED_ATTACK=.TRUE.. Additional parameters that can be used to fine tune the extended attack model are:

B_SDI                      = 1.0
DT_EXTENDED_ATTACK         = 3600.
AREA_NO_CONTAINMENT_CHANGE = 10000.0
MAX_CONTAINMENT_PER_DAY    = 100.0
SDI_FACTOR                 = 1.0
USE_SDI                    = .FALSE.
USE_SDI_LOG_FUNCTION       = .FALSE.